All posts
Formatting serial streams in hardware
12 August 2024 (programming haskell clash fpga)I've been playing around with building a Sudoku solver circuit on an FPGA: you connect to it via a serial port, send it a Sudoku grid with some unknown cells, and after solving it, you get back the solved (fully filled-in) grid. I wanted the output to be nicely human-readable, for example for a 3,3-Sudoku (i.e. the usual Sudoku size where the grid is made up of a 3 ⨯ 3 matrix of 3 ⨯ 3 boxes):
4 2 1 9 5 8 6 3 7 8 7 3 6 2 1 9 5 4 5 9 6 4 7 3 2 1 8 3 1 2 8 4 6 7 9 5 7 6 8 5 1 9 3 4 2 9 4 5 7 3 2 8 6 1 2 8 9 1 6 4 5 7 3 1 3 7 2 9 5 4 8 6 6 5 4 3 8 7 1 2 9
This post is about how I structured the stream transformer that produces all the right spaces and newlines, yielding a clash-protocols based circuit.
Continue reading »Shocking Finale
30 October 2023 (programming retrochallenge retrochallenge2023 retro homelab)Sunday, 15th October. Day of the HomeLab-2 game jam deadline. My port of The Revenge, or at least its first half, is fully playable. It even has quicksaving/loading implemented, with an in-memory buffer. Unfortunately, I didn't have time to find out what it would entail to implement persistent saving on cassette, but at least with quicksaving you can play cautiously enough to avoid frustrating deaths.
But can you actually win the game? To make sure you can, I wanted to play through from start to finish, using the hacked-up game scripts I ended up with that has a lot of the locations and scripts stripped. I could have just played the whole thing on a HomeLab-2 emulator, but I wanted something a bit more streamlined for two reasons:
- Because of the horrible foil keyboard of the real HomeLab-2, the firmware's keyboard sensing is a bit flakey when emulated on modern hardware with precise keypress detection, and so it's common to end up with unwanted key repetitions.
- If it turns out there's some flaw in the game scripts somewhere in the middle, I didn't want to replay the whole game from scratch after fixing the bug, reassembling and then reloading it into the emulator.
There and Back Again
27 October 2023 (programming retrochallenge retrochallenge2023 retro homelab)So here we are, with a couple days to go until the deadline, with a text adventure game that is roughly 22 KB in size, targeting a machine with 16 KB of RAM.
One thing to try would be to start trimming content. This is a straightforward idea: if we can remove messages and pieces of the script, then the size goes down. We know that the "empty" game (i.e. just the engine plus its runtime memory usage) is 2 KB, so by the intermediate value theorem, if we remove enough content, the size at some point will get below 16 KB.
But removing content from a text adventure game is not as easy as it might first sound, if you only have a couple days remaining to do that plus finish the engine plus do enough testing to make sure the game can still be finished. The reason for that is that most of the rooms, almost all objects, and most possible interactions are all there as part of some puzzle, with the whole game's start and end connected through a chain of the puzzles. Remove something and you might break a link and make the game unplayable. Perhaps even worse is if technically it doesn't become unplayable, but you remove something that contains the crucial information that would prompt the player to come up with a solution, and thus instead of a puzzle, now you have a "guess the random input you need to type in" game.
The other way to make the game smaller is to cut it in half: take some mid-point event, and turn that into the winning condition. This should allow you to remove all the rooms that are normally available only after that mid-point event; then, you can remove the scripts that are keyed to the removed rooms; and then you can remove the messages that are not referenced by the remaining scripts anymore.
To pull this off, you need a good middle point that makes sense as the new game not just technically, but narratively as well. Luckily, I've found such a point in The Revenge. So the original game's plot (spoiler alert for a 35-year-old Hungarian text adventure game!) is that random Japanese rural dude is sent to fetch water, arrives back to find his village razed and burned by some evil local warlord, and swears revenge (TITLE DROP!). Goes to the city, finds the warlord's mansion, but surprise surprise, it's heavily guarded. So after some local adventuring the protagonist ends up on a ship to China, living in a monastery for a while acquiring stamina through rigorous exercise, then learns kung-fu from an old master whose daughter he saves from bandits. Armed with deadly fists, he returns to Japan on a perilious trek through shark-infested waters on a dinghy, infiltrates the mansion and finally confronts the evil warlord. Standard kung-fu B movie plot.
On the one hand, the good news is that there is a very natural way to split this into two episodes: the first episode can end with the protagonist learning kung-fu, leaving the actual confrontation with the Big Bad to the second episode. On the other hand, as you can see from this structure, you don't actually get to remove half the locations by just keeping half the game, because the second half mostly consists of coming back to Japan and revisiting the same places, just now with the ability to defeat opponents in hand-to-hand combat.
On the gripping hand, we don't need to cut down our memory usage by half -- we just need to reduce it by 6 KB, or 30% of our original 20 KB asset size. That should be doable.
For the technical details, the idea is the following. First of all, let's briefly look at what the game script looks like. Here's some example bytecode that scripts a single interactive response.
1d Length of second room's scripts, for easy indexing
10 Length of next script, for easy skipping if the input doesn't match
3a 78 00 Matches user input consisting of word 3a "fill" and 78 "bucket"
08 78 02 If item 78 is not here (in inventory or in current room), print message 2 and end
06 0a 29 If variable 0a is not 0, print message 29 and end
04 0a Set variable 0a to ff
02 04 Print message 4
14 0b Play chime 0b
00 End
05 Length
33 a4 00 Input: 33 "swim" a4 "river"
0c 03 Go to location 03 "island"
04 Length
02 00 Input: 02 "northeast"
0c 04 Go to location 04 "hillside above village"
00 End of handlers for room 2
15 Length of room 3's handlers
... Room 3's script(I should note here that since my HomeLab-2 version has no "multimedia", all bytecode operations like show picture P or play chime C are stripped during conversion.)
Now let's suppose we wanted the game to end in this room without the ability to progress to the island. We can remove the second handler in its entirety (saving 6 bytes in the process), and then statically re-traverse the remaining bytes to find all go to location X commands. When viewing the result as a directed graph, we will see that room 03 is no longer reachable from the starting location, and so we can throw away the script in the next 22 (including the length) bytes. Then we can build similar accessibility information from the remaining bytecode, this time not for the rooms, but for the messages. For example, message 29 is definitely needed (since it is referenced in room 2), but there might be other messages that are only referenced in the 22 bytes we've just thrown away.
By the way, for some eye candy, here's what the map looks like. The left-hand side shows the original map. Rooms 8 to 13 and 70 to 76 comprise two of those super annoying mazes that old text adventure games were keen to include. The right-hand side shows the map of The Revenge Episode 1, i.e. my cut-in-half HomeLab-2 version. Simplifying the episode one maze didn't really save much space since all the constituent rooms use the same text descriptions, but I think skipping them simply makes the game better.
Of course, there are also location-agnostic interaction scripts involving carriable items; since with the changes to the map, I already fit into memory (if just barely), and time was quickly running out, I decided not to bother pruning the scripting of items that are not aquirable in the first half of the game.
So I had a fully playable game with even enough space left to implement a simple in-memory gamestate saving facility, which is useful because there are quite some lethal situations in the game. At this point I had one day (a Sunday) remaining, and I thought it was going to be smooth sailing: my plan was to play through the modified script in a desktop interpreter (with replaying and checkpointing capabilities) to make sure the game is winnable, convert it to a WAV file for deployment, and send it in.
Join me in the next post to read why that last day was anything BUT smooth sailing. DUN DUN DUUUUUUUUUUN!

An Idea for a Grand Adventure
24 October 2023 (programming retrochallenge retrochallenge2023 retro c64 homelab)Two weeks before the game jam deadline, I finally had the idea for my main entry. But with most of the first week occupied with work and travel, will the second week be enough to make it a reality?
Years ago, after remaking Time Explorer, I went on to reverse-engineer István Rátkai's subsequent games for the Commodore 64: The Revenge, and New Frontier I and II. This work culminated in a crowd-funded modern Android release. These Android versions were possible because these text adventure games, in quite forward-looking way for 1988, were originally written in a small homebrew bytecode language that was then packaged up with an interpreter. Think of it like a very primitive version of Infocom's Z-machine, but without all the Lisp-y sensitivities.
So anyway, my idea was to take the game's scripts as-is, and implement my own bytecode interpreter for the HomeLab-2. The Commodore 64 has 64 KB of RAM, while the HomeLab only has 16; but surely if I get rid of the multimedia (the per-room graphics and the small handful of short melodies played at key points of the games), the remaining text and scripts can't be that much?
Well it turns out when talking about text adventure games for 8-bit home computers, all that text is actually relatively quite a lot! In The Revenge, for example, just the various messages printed throughout the game fill 16 KB, and then we have 10 more KB of the recognized words and the game script. Clearly, this 26 KB of data will not fit into 16 KB, especially not leaving enough space for the game engine itself and the 256 bytes of game state.
Well, what if we try to be a bit more clever about representation? For example, because of the HomeLab-2's fixed upper-case character set, all that text will be in upper-case and without using any Hungarian accented characters, so we can use something similar to ZSCII to store 3 characters in 2 bytes. This, and some other small tricks like encoding most message-printing in just a single byte instead of a byte to signal that this is message-printing followed by the byte of the message ID, gets us to below 20 KB. Still not good, but better!
It was at this point that I also started writing the engine, to see how big that will be. Of course, at this point I was only able to try it out by only including a subset of the rooms and the game script, but at least it allowed me to get a size estimate for it. And so it came to about 1.5 KB of code to implement everything, plus 256 bytes of game state. Optionally, if we have space left, we can use a second 256 bytes to implement quicksave/quickload.
So what will we do with our budget of 14 KB, given a 20 KB game? Let's find out in the next post.
Getting my HomeLab-2 sea legs
21 October 2023 (homelab programming retrochallenge retrochallenge2023 retro haskell)Previously, we left off our HomeLab-2 game jam story with two somewhat working emulators, and a creeping realization that we still haven't written a single line of code.
Actually, it was a bit worse than that. My initial "plan" was to "participate in the HomeLab-2 game jam", with nothing about pesky details such as:
- What game do I want to make?
- What technology will I use?
- How will I find time to do it, given that I'm spending all of September back home in Hungary?
I found the answers to these questions in reverse order. First of all, since for three of the five weeks I've spent in Hungary, I was working from home instead of being on leave, we didn't really have much planned for those days so the afternoons were mostly free.
Because the HomeLab-2 is so weak in its processing power (what with its Z80 only doing useful work in less than 20% of the time if you want to have video output), and also because I have never ever done any assembly programming, I decided now or never: I will go full assembly. Perhaps unsurprisingly, perhaps as a parody of myself, I found a way to use Haskell as my Z80 assembler of choice.
This left me with the question of what game to do. Coming up with a completely original concept was out of the quesiton simply because I lack both the game designing experience as well as ideas. Also, if there's one thing I've learnt from the Haskell Tiny Games Jam, it is that it's better to crank out multiple poor quality entries (and improve in the process) than it is to aim for the stars (a.k.a. that pottery class story that is hard to find an authoritative origin for). Another constraint was that neither of my emulators supported raster graphics, and I was worried that even if they did, it would be too slow on real hardware; so I wanted to come up with games that would work well with character graphics.
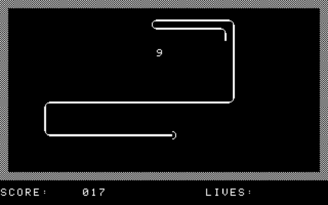
After a half-hearted attempt at Tetris (which I stopped working on when someone else has already submitted a Tetris implementation), the first game I actually finished was Snake. For testing, I just hacked my emulator so that on boot, it loads the game to its fixed stating address, then used CALL from HomeLab BASIC to start it. This was much more convenient than loading from WAV files; doubly so because it took me a while to figure out how exactly to generate a valid WAV file. For the release version, I ended up going via an HTP file (a byte-level representation of the cassette tape contents) which is used by some of the pre-existing emulators. There's an HTP to WAV converter completing the pipeline.
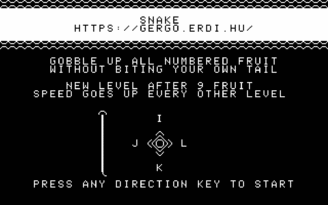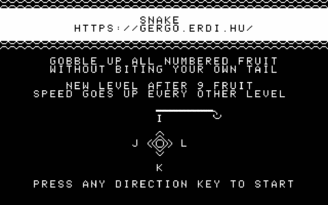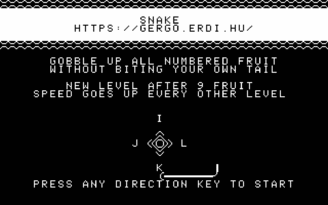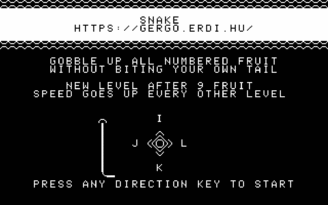
There's not much to say my Snake. I tried to give it a bit of an arcade machine flair, with an animated attract screen and some simple screen transitions between levels. One of the latter was inspired by Wolfenstein 3D's death transition effect: since the textual video mode has 40×25 characters, a 10-bit maximal LFSR can be used as a computationally cheap way of replacing every character in a seemingly random (yet full-screen-covering) way.
For my second entry, I went with 2048. Shortly after finishing Snake, thanks to Gábor Képes I had the opportunity to try a real HomeLab-2 machine. Feeling how unresponsive the original keyboard is convinced me that real-time games are not the way to go.
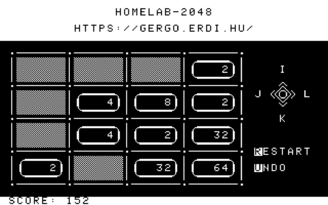
The challenge with a 2048-like game on a platform like this is that you have to update a large portion of the screen as the tiles slide around. Having an assembler that is an EDSL made it a breeze to try various speedcoding techniques, but with lots of tiles sliding around, I just couldn't get it to fit within the frame budget, which led to annoying flickering as a half-finished frame would get redrawn before the video refreshing interrupt handler eventually returned to finish the rest of the frame. So I ended up using double buffering, which technically makes each frame longer to draw, but avoids inconsistent visible frames.
Since the original 2048 is a product of modern times, I decided to pair my implementation with a more clean design: just like a phone app, it boots straight into the game with no intro screen, with all controls shown right on the main screen.
Between these two games, and all the other fun stuff one doesn when visiting home for a month, September flew by. As October approached, I stumbled upon this year's RetroChallenge announcement and realized the potential for synergy between doing something cool in a last hurrah before the HomeLab-2 game jam deadline and also blogging about it for RetroChallenge. But this meant less than two weeks to produce a magnum opus. Which is why this blogpost series became retrospective — there was no way to finish my third game on time while also writing about it.
But what even was that third and final game idea? Let's find out in the next post.
Older posts:
- 18 October 2023: So... HomeLab-2? What is that?
- 16 October 2023: Another year, another RetroChallenge
- 2 July 2022: A small benchmark for functional languages targeting web browsers
- 2 May 2022: Cheap and cheerful microcode compression
- 18 September 2021: Rust on the MOS 6502: Beyond Fibonacci
- 17 November 2020: A tiny computer for Tiny BASIC
- 15 September 2020: A "very typed" container for representing microcode
- 1 August 2020: Solving text adventure games via symbolic execution
- 7 May 2020: Integrating Verilator and Clash via Cabal
- 30 September 2018: Composable CPU descriptions in CλaSH, and wrap-up of RetroChallenge 2018/09
- 23 September 2018: CPU modeling in CλaSH
- 22 September 2018: Back in the game!
- 15 September 2018: Very high-level simulation of a CλaSH CPU
- 8 September 2018: PS/2 keyboard interface in CλaSH
- 2 September 2018: CλaSH video: VGA signal generator
- 29 August 2018: RetroChallenge 2018: CHIP-8 in CλaSH
- 12 May 2017: Rust on AVR: Beyond Blinking
- 21 February 2016: Stack reification via trampolines
- 28 December 2015: Hacks of 2015
- 5 June 2015: Időrégész 2015
- 2 March 2015: Initial version of my Commodore PET
- 5 February 2015: Typed embedding of STLC into Haskell
- 12 July 2014: Arrow's place in the Applicative/Monad hierarchy
- 29 March 2014: My first computer
- 31 December 2013: Brainfuck on the Commodore 64
- 5 October 2013: Yo dawg I heard you like esoteric programming languages...
- 1 May 2013: Simply Typed Lambda Calculus in Agda, Without Shortcuts
- 17 February 2013: Write Yourself a Haskell... in Lisp (3 comments)
- 19 January 2013: A Brainfuck CPU in FPGA (3 comments)
- 1 December 2012: Static analysis with Applicatives
- 11 March 2012: Basics for a modular arithmetic type in Agda
- 19 February 2012: Mod-N counters in Agda (6 comments)
- 3 December 2011: How I learned about Java's lack of type erasure the hard way
- 5 November 2011: Bali (3 comments)
- 24 July 2011: Még élek... (1 comment)
- 23 May 2011: Érkezés (9 comments)
- 19 May 2011: Úti élmények (5 comments)
- 16 May 2011: I'm leaving on a jet plane... (6 comments)
- 3 March 2011: Gettó-szakállvágó
- 13 February 2011: Developing iPhone applications in Haskell — a tutorial (5 comments)
- 18 November 2010: Pom-pom poporopo-pom (4 comments)
- 23 October 2010: The case for compositional type checking (1 comment)
- 2 October 2010: Logicomix
- 7 September 2010: From Register Machines to Brainfuck, part 2
- 6 September 2010: From Register Machines to Brainfuck, part 1
- 23 May 2010: Efficient type-level division for Haskell (1 comment)
- 16 May 2010: Compiling Haskell into C++ template metaprograms
- 19 April 2010: Unary arithmetics is even slower than you'd expect
- 15 March 2010: Neked aztán lehet (1 comment)
- 3 March 2010: Internet-celebritás lettem... (1 comment)
- 22 February 2010: The B Method for Programmers (Part 2)
- 16 February 2010: The B Method for Programmers (Part 1)
- 8 February 2010: The downfall of Soviet microprocessor technology and Lisp
- 1 December 2009: Adventi Menger-szivacs (4 comments)
- 20 July 2009: Ember a Holdon! (7 comments)
- 29 May 2009: Grand Slam (8 comments)
- 7 May 2009: Relativisztikus hiperszámítógépek (5 comments)
- 24 March 2009: Titanic 2009 itiner (4 comments)
- 20 March 2009: Odüsszeisz-fázis
- 17 March 2009: Eliminating magic strings from ELisp's (interactive)
- 3 March 2009: Composite pattern a gyakorlatban (3 comments)
- 25 February 2009: λ: A tiltott kalkulus (1 comment)
- 22 January 2009: Type inference for CLazy (1 comment)
- 12 January 2009: CLazy interpreter and compiler (1 comment)
- 18 December 2008: Pierre Basieux: Top 7 (1 comment)
- 17 October 2008: Generikus programozás (5 comments)
- 21 September 2008: Hacktivity 2008 (7 comments)
- 15 September 2008: Viki in a nutshell (5 comments)
- 4 September 2008: Programozás visszavezetéssel (4 comments)
- 17 August 2008: Geekparty és egy breaking news (3 comments)
- 7 August 2008: Konzolok vs. HDTV-k (2 comments)
- 15 July 2008: Hiányzó iWiW feature (8 comments)
- 6 July 2008: A titkosügynökök magányossága (2 comments)
- 17 June 2008: Mark all as read (4 comments)
- 2 June 2008: Incompetent fuckwits (3 comments)
- 26 May 2008: Indi János és az ajkai kristályszuvenírek (9 comments)
- 25 May 2008: Tooltips for SLIME
- 18 May 2008: Nyomkodom a "Műköggyé" gombot (3 comments)
- 11 May 2008: A hétvége rendeltetésszerű használata (4 comments)
- 23 April 2008: Iskola az őrület határán
- 21 April 2008: Munkamorál (2 comments)
- 16 April 2008: Structure and Interpretation of Computer Programs
- 13 April 2008: Titanic: Szamócás süti
- 11 April 2008: Zuboly-koncert
- 11 April 2008: Cruisin' with me main man (1 comment)
- 8 April 2008: Titanic: Fél Nelson
- 4 April 2008: Titanic: Lesipuskás
- 28 March 2008: An important milestone (3 comments)
- 21 March 2008: Így lopjunk evőeszközt (3 comments)
- 6 February 2008: Look at me, I'm Dr. Zoidberg, home-owner! (1 comment)
- 1 February 2008: Alternatív WRT firmware-ek (3 comments)
- 9 January 2008: Egy nem PC asszociáció
- 28 December 2007: Egy eseménymentes hét
- 20 December 2007: Reál balfasz (3 comments)
- 9 December 2007: Azt hiszem, jól vagyok tartva (1 comment)
- 6 December 2007: Mikulás (4 comments)
- 14 November 2007: Not worth the paper it's printed on
- 10 November 2007: Diviánszky Péter for prezident!
- 30 October 2007: Nintendo a seggem (9 comments)
- 27 October 2007: Sapkakiválasztási axióma (15 comments)
- 15 October 2007: Jönnek a letölthető Wii demók? (3 comments)
- 12 October 2007: K stands for Kwality (6 comments)
- 7 October 2007: Egy jó doboz bármit elad
- 3 October 2007: Valós halál (10 comments)
- 15 September 2007: Élelmiszertúladagolás
- 5 September 2007: Folytatásos könyvek a bábeli könyvtárban (1 comment)
- 3 August 2007: Pókmalac, pókmalac... (3 comments)
- 2 August 2007: A kindergarten of pancakes
- 18 July 2007: Quote és backquote fia vagyok én (2 comments)
- 12 July 2007: Autósmozi (1 comment)
- 8 July 2007: Goblin
- 14 June 2007: Foglalkozása: aranytestű rock-isten (4 comments)
- 28 May 2007: Orvosi segítségre van szükségem
- 18 May 2007: Encsé, az élet császára (1 comment)
- 11 May 2007: Merre megy a matematika? (1 comment)
- 26 April 2007: Ég a fater^H^Hörzs! (1 comment)
- 11 April 2007: Kampány
- 29 March 2007: Félelem és reszketés Hamburgban (6 comments)
- 17 March 2007: Interactivity and Games as an Artform (9 comments)
- 16 March 2007: Encsé leverte a köcsögöket (5 comments)
- 26 February 2007: Az áltudós az becsap árvíz aszály tájfun lecsap!! (8 comments)
- 15 February 2007: Statisztikai vizualizáció rizsszemekkel (9 comments)
- 11 February 2007: Wii buli Warioval és Raymannel (3 comments)
- 9 February 2007: Szóval a Wii-ről (32 comments)
- 2 February 2007: Random sirám (3 comments)
- 21 January 2007: Ami a Wii használati utasításából kimaradt
- 29 December 2006: Playstation retrospektív: Gran Turismo (6 comments)
- 27 December 2006: Kis- és nagykarácsonyok
- 11 December 2006: Kamera által, homályosan (5 comments)
- 28 November 2006: Sziget a Google Earth-on (1 comment)
- 22 November 2006: Commenting on blog entries (2 comments)
- 8 November 2006: Ruby on Rails a seggem
- 6 November 2006: Újra itthon...
- 4 November 2006: Utazás Absztinenciába
- 2 November 2006: Képernyőregények
- 17 October 2006: A hallgató, akinek semmi sem kerülte el a figyelmét
- 13 October 2006: Activity log
- 11 October 2006
- 8 October 2006: Registering Windows file types with NSIS (2 comments)
- 2 October 2006: RSS feeds to ease transition from Advogato
- 22 September 2006: Queueing timeouts in JavaScript
- 12 September 2006: Tombol a kompetencia
- 10 September 2006: VPG 20 (2 comments)
- 9 September 2006: Luggage space extravaganza (1 comment)
- 27 August 2006: Mad Maestro
- 21 August 2006: Tilos 15 (1 comment)
- 13 August 2006: Sziget, bazmeg
- 8 August 2006: Papírmentes iroda
- 19 July 2006: The following takes place between 10:00 a.m. and 6:00 p.m. (2 comments)
- 24 June 2006: Programming by Google
- 16 June 2006: Éjjeli áramszünet
- 14 June 2006: Microsoft Natural Keyboard 4000
- 12 May 2006: Legközelebb eladok neki egy toronyórát, lánccal
- 8 May 2006: π DVD (4 comments)
- 7 May 2006: Mi ez itten ez?
- 18 May 2005: Dension customer support: A+
- 2 May 2005: Chrome rings (1 comment)
- 24 April 2005
- 25 March 2005
- 11 March 2005
- 8 March 2005: I think I've found it