This post is about an optimization to the Intel 8080-compatible
CPU that I describe in detail in my book Retrocomputing in
Clash. It didn't really fit anywhere in the book, and it
isn't as closely related to the FPGA design focus of the book,
so I thought writing it as a blog post would be a good idea.

Just like the
real 8080 from 1974, my Clash
implementation is microcoded: the semantics of each machine
code instruction of the Intel 8080 is described as a sequence of
steps, each step being the machine code instruction of an even
simpler, internal micro-CPU. Each of these micro-instruction
steps are then executed in exactly one clock cycle each.
My 8080 doesn't faithfully replicate the hardware 8080's
micro-CPU; in fact, it doesn't replicate it at all. It is a
from-scratch design based on a black box understanding of the
8080's instruction set, and the main goal was to make it easy to
understand, instead of making it efficient in terms of FPGA
resource usage. Of course, since my micro-CPU is different, the
micro-instructions have no one to one correspondence with the
orignal Intel 8080, and so the microcode is completely different
as well.
In the CPU, after fetching the machine code instruction byte, we
look up the microcode for that byte, and then execute it cycle
by cycle until we're done. This post is about how to store that
microcode efficiently.
An illustrative example
To avoid dealing with the low-level details of what exactly goes
on in our microcode, for the rest of this blog post let's use a
dictionary of a small handful of English words as our running
example. Suppose that we want to store the following table:
0. shape
1. shaping
2. shift
3. shapeshifting
4. ape
5. aping
6. ship
7. shipping
8. grape
9. elope
10. shard
11. sharding
12. shared
13. geared
There's a lot of redundancy between these words, and we will see
how to exploit that. But does this make it a poor example that
won't generalize to our real use case of storing microcode? Not
at all. There are lots of 8080 instructions that are just
minimal variations of each other, such as doing the exact same
operation but on different general purpose registers; thus,
their microcode is also going to be very similar, doing the same
setup/teardown around a different kernel.
Fixed length vectors
Since our eventual goal is designing hardware, everything
ultimately needs a fixed size. The most straightforward
representation of our dictionary, then, is as a vector that is
sized to fit the longest single word:
type Dictionary = Vec 14 (Vec 13 Char)
The longest word "shapeshifting" is 13 characters.
For all 14 possible inputs, we store 13 characters, using a
special "early termination" marker like '.' in
the middle for those words that are shorter:
0. shape........
1. shaping......
2. shift........
3. shapeshifting
4. ape..........
5. aping........
6. ship.........
7. shipping.....
8. grape........
9. elope........
10. shard........
11. sharding.....
12. shared.......
13. geared.......
We can then use this table very easily in a hardware
implementation: after fetching the "instruction", i.e. the
dictionary key, we look up the corresponding Vec 13
Char in the dictionary ROM, and keep a 4-bit counter of
type Index 13 to process it cycle by cycle.
This is the equivalent of the microcode representation that we
use in Retrocomputing in Clash, but it is easy to
see that it is very wasteful. In our illustrative example, we
store a total of 14 ⨯ 13 = 182 characters, whereas the total
length of all strings is only 85, so we waste about 55% of our
storage.
On our 8080-compatible CPU we get similar (slightly worse)
numbers: the longest instruction, XTHL, takes 18
cycles. We don't need to store microcode for the first cycle,
since that always corresponds to just fetching the instruction
byte itself. This leaves us with 17 micro-operations. For all
256 possible machine code instruction bytes, we end up storing a
total of 256 ⨯ 17 = 4352 micro-operations, but if we look at the
cycle
count of each individual 8080 instruction, the useful part
is only 1493 micro-operations. That's a waste of about 65%.
Using terminators

No, wait, not this guy.
The obvious way to cut down on some of that fat is to store each
word only up to its end. We can use a terminated
representation for this, by keeping some end-of-word marker
('.' in the examples below), and concatenating all
items:
0. shape.
6. shaping.
14. shift.
20. shapeshifting.
34. ape.
38. aping.
44. ship.
49. shipping.
58. grape.
64. elope.
70. shard.
76. sharding.
85. shared.
92. geared.
Instead of storing 182 characters, we now only store 99. While
this is still more than 85, because we also have to store all
those word-separating '.' markers, it is still a
big improvement.
However, there's a bit of cheating going in here, because with
the above table as given, we'd have no way of looking up words
by their original index. For example, word #7 is
shipping, but if we started at entry number 7 in
this representation, we'd get haping. We need to
also store a table of contents that gives us the
starting address of each dictionary entry:
0. 0
1. 6
2. 14
3. 20
4. 34
5. 38
6. 44
7. 49
8. 58
9. 64
10. 70
11. 76
12. 85
13. 92
If we want to calculate the contribution of the table of
contents to the total size, we have to get a bit more
precise. Previously, we characterized ROM footprint in units of
characters, but now we need to store 7-bit indices as well. To
be able to add the two together, we need to also fix the bit
width of each character. For now, let's just use 8 bits per
character.
The total size in bits, for storing the table of contents and
the dictionary in terminated form, comes out to 14 ⨯ 7 + 99
⨯ 8 = 890. We can compare this to the 14 ⨯ 13 ⨯ 8 = 1456 bits of
the fixed-length representation to see that it's a huge
improvement.
Linked lists

Not this guy either.
As we've seen, the table of contents takes up 98 bits, or about
11% of our total footprint in the terminated representation. Can
we get rid of it?
One way of doing this is to change the starting address of each
word to its key. This is already the case for our first word,
shape, since its key is 0 and it starts at address
0. However, the next word, shaping, can't start at
address 1, since that is where the second letter of the first
word resides.
If we store the next character's address instead of making the
assumption that it's going to be the next address, we can start
each word at the address corresponding to its key, and then
leave subsequent letters to addresses beyond the largest key:
0. s → @14
1. s → @18
2. s → @24
3. s → @28
4. a → @40
5. a → @42
6. s → @46
7. s → @49
8. g → @56
9. e → @60
10. s → @64
11. s → @68
12. s → @75
13. g → @80
14. h → a → p → e → @85
18. h → a → p → i → n → g → @85
24. h → i → f → t → @85
28. h → a → p → e → s → h → i → f → t → i → n → g → @85
40. p → e → @85
42. p → i → n → g → @85
46. h → i → p → @85
49. h → i → p → p → i → n → g → @85
56. r → a → p → e → @85
60. l → o → p → e → @85
64. h → a → r → d → @85
68. h → a → r → d → i → n → g → @85
75. h → a → r → e → d → @85
80. e → a → r → e → d → @85
Not only did we get rid of the table of contents, we can also
store the terminators more implicitly, by using a special value
for the next pointer. In this example, we can use @85 for that
purpose, pointing beyond the last cell. This leaves us with just
85 cells compared to the 99 cells with terminators.
However, each cell now contains both a character and a
pointer. Since we need to address 85 cells, the latter takes up
7 bits, for a total of 85 ⨯ (8 + 7) = 1275 bits.
This is a step back from the the terminated representation's 890
bits. We can make a note, though, that if each character was at
least 35 bits wide instead of 8, the linked representation would
come out ahead. But the real reason we are interested in the
linked-list form is that it suggests a further optimization that
finally exploits the redundancy between the words in our
dictionary.
Common suffix elimination
This is where we get to the actual meat of this post. Let's
focus on the following subset of our linked list representation:
12. s → @75
13. g → @80
75. h → a → r → e → d → @85
80. e → a → r → e → d → @85
We are storing the shared suffix ared twice, when
instead, we could redirect the second one to the first
occurrence, saving 4 cells:
12. s → @75
13. g → @80
75. h → @76
76. a → r → e → d → @85
80. e → @76
If we apply the same idea to all words, we arrive at the
following linked representation. Note that we still start every
word at the index corresponding to its key, avoiding the need
for a table of contents:
0. s → @14
1. s → @15
2. s → @16
3. s → @20
4. a → @32
5. a → @34
6. s → @35
7. s → @38
8. g → @41
9. e → @42
10. s → @44
11. s → @48
12. s → @52
13. g → @56
14. h → @4
15. h → @5
16. h → i → f → t → @57
20. h → a → p → e → s → h → i → f → t → @29
29. i → n → g → @57
32. p → e → @57
34. p → @29
35. h → i → p → @57
38. h → i → p → @34
41. r → @4
42. l → o → @32
44. h → a → r → @47
47. d → @57
48. h → a → r → d → @29
52. h → @53
53. a → r → e → @47
56. e → @53
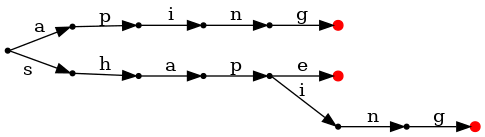
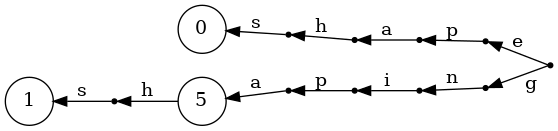
It's hard to see what exactly is going on here from this textual
format, but things become much cleaner if we display it as a
graph:

We can compute the size of this representation along the same
lines as the linked-list one, except now we only have 57
cells. This also means that the pointers can be 6 bits instead
of 7, for a total size of 57 ⨯ (8 + 6) = 798 bits. A 10% save
compared to the 890 bits of the terminated representation!
Going back to our real-world use case of 8080 microcode, each
micro-instruction is 15 bits wide. We have already computed that
the fixed-length representation uses 4352 ⨯ 15 = 65,280 bits; if
we do the same calculation for the other representations, we get
28,286 bits in the terminated representation, 37,492 bits with
linked lists, and a mere 13,675 bits, that is, just 547 cells,
with the common suffixes shared!
So how do we compute this shared-suffix representation? Luckily,
it turns out we can do that in just a handful of lines of code.
Reverse trie representation
To come up with the basic idea, let's start by thinking about
why we are aiming to share common suffixes instead of common
prefixes, such as the prefix between shape and
shaping. The answer, of course, is that we need to
address each word separately. If we try to unify
shape and shaping, starting with the
key 0 or 1 and making it as far as shap doesn't
tell us on its own if we should continue with e or
ing for the given key.
On the other hand, once we start a given word, it doesn't matter
where subsequent letters are, including even the beginning of
other words (as is the case between shaping and
aping). So fan-out is bad (it would mean having to
make a decision), but fan-in is a-OK.
There's an obvious data structure for exploiting common
prefixes: we can put all our words in a trie. We can make one in
Haskell by using a finite map from the next key element to the
stored data (for terminal nodes) and the rest of the trie:
import Data.List.NonEmpty (NonEmpty(..))
import qualified Data.List.NonEmpty as NE
import qualified Data.Map as M
newtype Trie k a = MkTrie{ childrenMap :: M.Map k (Maybe a, Trie k a) }
children :: Trie k a -> [(k, Maybe a, Trie k a)]
children t = [(k, x, t') | (k, (x, t')) <- M.toList $ childrenMap t]
Note that a terminal node doesn't necessarily mean no children,
since one full key may be a proper prefix of another key. For
example, if we build a trie that stores "FOO" ↦ 1
and "FOOBAR" ↦ 2, then the node at 'F' → 'O'
→ 'O' will contain value Just 1 and also the
child trie for 'B' → 'A' → 'R'.
The main operation on a Trie that we will need is building one
from a list of (key, value) pairs via
repeated insertion:
empty :: Trie k a
empty = MkTrie M.empty
insert :: (Ord k) => NonEmpty k -> a -> Trie k a -> Trie k a
insert ks x = insertOrUpdate (const x) ks
insertOrUpdate :: (Ord k) => (Maybe a -> a) -> NonEmpty k -> Trie k a -> Trie k a
insertOrUpdate f = go
where
go (k :| ks) (MkTrie ts) = MkTrie $ M.alter (Just . update . fromMaybe (Nothing, empty)) k ts
where
update (x, t) = case NE.nonEmpty ks of
Nothing -> (Just $ f x, t)
Just ks' -> (x, go ks' t)
fromList :: (Ord k) => [(NonEmpty k, a)] -> Trie k a
fromList = foldr (uncurry insert) empty
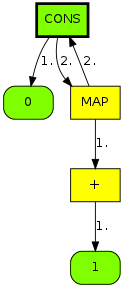
Ignoring the actual indices for a moment, looking at a small
subset of our example consisting of only shape,
shaping, and aping, the trie we'd
build from it looks like this:
But we want to find common suffixes, not prefixes, so how does
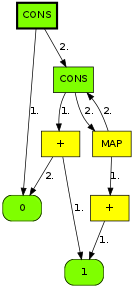
all this help us with that? Well, a suffix is just a prefix of
the reversed sequence, so watch what happens when we build a
trie after reversing each word, and lay it out left-to-right:

In this representation, terminal nodes correspond to
starting letters of each word, so we can store the
dictionary index as the value associated with them:
At this point, it should be clear how we are going to build our
nicely compressed representation: we build a suffix trie, and
then flatten it by traversing it bottom up. Before we do that,
though, let's take care of one more subtlety: what if we have
the same word at multiple indices in our dictionary? This is not
an invalid case, and does come up in practice for the multiple
NOP instructions of the 8080, all mapping to the
exact same microcode. The solution is to simply allow a
NonEmpty list of dictionary keys on terminal nodes
in the resulting trie:
fromListMany :: (Ord k) => [(NonEmpty k, a)] -> Trie k (NonEmpty a)
fromListMany = foldr (\(ks, x) -> insertOrUpdate ((x :|) . maybe [] NE.toList) ks) empty
suffixTree :: (KnownNat n, Ord a) => Vec n (NonEmpty a) -> Trie a (NonEmpty (Index n))
suffixTree = fromListMany . toList . imap (\i word -> (NE.reverse word, i))
Flattening
The pipeline going from a suffix tree to flat ROM payload
containing the linked-list representation has three steps:
-
Allocate an address to each cell, and fill in the links. We
can make our lives much easier by using Either (Index n)
Int for the addresses: Left i is an index
from the original dictionary, and Right ptr means
it corresponds to the middle of a word.
-
Renumber the addresses by reserving the first n
addresses to the original indices (remember, this is how we
avoid the need for a table of contents), and using the rest
for the internal ones.
-
After step two we have a single continuous address block of
cells. All that remains to be done is reordering the
elements, sorting each one into its own position.
compress :: forall n a. (KnownNat n, Ord a) => Vec n (NonEmpty a) -> [(a, Maybe Int)]
compress = reorder . renumber . links . suffixTree
where
reorder = map snd . sortBy (comparing fst)
renumber xs = [ (flatten addr, (x, flatten <$> next)) | (addr, x, next) <- xs ]
where
offset = snatToNum (SNat @n)
flatten (Left k) = fromIntegral k
flatten (Right idx) = idx + offset
Since we don't know the full size of
the resulting ROM upfront, we have to use Int as
the final unified address type; this is not a problem in
practice since for our real use case, all this microcode
compression code runs at compile time via Template Haskell, so
we can dynamically compute the smallest pointer type and just
fromIntegral the link pointers into that.
We conclude the implementation with links, the
function that computes the next pointers. The cell emitted for
each trie node should link to the cell for its parent node, so
we pass the parent down as we traverse the trie (this is the
next parameter below). The new cell itself is
either put in the next empty cell if it is not a terminal node,
i.e. if it doesn't correspond to a first letter in our original
dictionary; or, it and all its aliases are emitted at their
corresponding Left addresses.
links :: Trie k (NonEmpty a) -> [(Either a Int, k, Maybe (Either a Int))]
links = execWriter . flip runStateT 0 . go Nothing
where
go next = mapM_ (node next) . children
node next (k, mx, t') = do
this <- case mx of
Nothing -> Right <$> alloc
Just (x:|xs) -> do
tell [(Left x', k, next) | x' <- xs]
return $ Left x
tell [(this, k, next)]
go (Just this) t'
alloc = get <* modify succ
If you want to play around with this, you can find the full code on
GitHub; in particular, there's
Data.Trie
for the no-frills trie implementation, and
Hardware.Intel8080.Microcode.Compress
implementing the microcode compression scheme described in this post.
And finally, just for the fun of it, this is what the 8080
microcode — that prompted all this — looks like in its suffix
tree form, clearling showing the clusters of instructions that
share the same epilogue: