Write Yourself a Haskell... in Lisp

For me, the best way to understand something is usually to implement it myself. So when I first started getting serious about Haskell, I implemented (in Common Lisp) a simple lazy functional programming language that used graph rewriting for the interpretation. Then, years later, I mentioned this implementation in a Reddit thread about writing a Lisp interpreter in Haskell (maybe inspired by the well-known Haskell tutorial and this blogpost's namesake). I now decided to clean up that old code, throw out all the unnecessary cruft, and arrive at something easy to understand. The finished interpreter is less than 500 lines of Common Lisp (not including the type checker which will be the subject of my next post).

I should also add that of course we're not going to actually implement Haskell here. As we'll see, the language is a very much simplified model of pure, lazy functional languages. It's actually closer to GHC's Core than Haskell.

Syntax

We're not going to bother with parsing: our input programs will be S-expressions. For example, instead of the following Haskell program:

data List a = Nil | Cons a (List a)

map f Nil = Nil
map f (Cons x xs) = Cons (f x) (map f xs)
      

we will write:

(defdata list (a) nil (cons a (list a)))

(deffun map
   ((f nil) nil)
   ((f (cons x xs)) (cons (f x) (map f xs))))
      

As you can see, there is no syntactic distinction between variable names and constructor names — when translating these S-expressions, we'll take special care to always register constructor names before processing expressions.

Internally, we'll represent programs in an even more simplified way, by making all function applications explicit. Multi-parameter functions and constructors, of course, will be implemented via schönfinkeling. The syntax tree itself is represented using two class hierarchies: subclasses of expr for expressions, and subclasses of pattern for patterns:

Going from S-expressions to this object-oriented representation is straightforward:

Graph rewriting semantics

The basic idea behind implementing a lazy functional language using graph rewriting is to represent terms as directed graphs, and reducing a function application is implemented by replacing the application node with the graph corresponding to the right-hand side of the function definition, of course with all the references to formal arguments instantiated to the actual arguments.

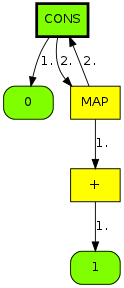
Let's look at a simple example first, with no sharing or recursion:

(defvar x
  (let ((primes (cons 2 (cons 3 (cons 5 nil)))))
    (map (+ (+ 1 1) primes))))
    

As you can see, the green boxes represent constructors (with rounded corners for primitive values), yellow ones are functions, and the small gray circles are function applications. There are no variables, since references are resolved when building this graph.

We can simplify this format by omitting application nodes and just pushing arguments under their function node (until it becomes saturated), like this:

Reducing this entails instantiating the following graph (from the second case of map), with f bound to (+ (+ 1 1), x bound to 2, and xs bound to (cons 3 (cons 5 nil)). Note the explicit application node: we won't know the arity of f until it's bound to something.

Resulting in

Note how the first argument to + is shared in the result. Also note how (+ (+ 1 1) 2) is not reduced by map, since it is lazy in its first argument.

Our second example shows recursively-defined terms:

(defvar nats (cons 0 (map (+ 1) nats)))
    

This is already in WHNF, but we can nevertheless reduce the tail of the list, to get this:

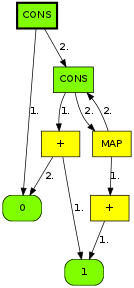
and so on.

Representing the graphs

Since we want to be able to replace function application subgraphs easily (when reducing those applications), the representation uses an extra level of indirection: gnodes contain the payload: the type of the node and pointers to its children grefs; and each gref contains a single reference to its content gnode. grefs can be shared, so when its content gnode is replaced, all the shared references are updated.

Variable nodes

Earlier, we said variables are not present as such in the graph representation, since they are inlined (respecting sharing, of course). But we still have a var-gnode class defined above. The reason for that is simply to mark occurances of formal variables in function definitions, which will be filled in when reducing function applications.

But there's another, more compilcated problem with variables. Our language's let construct is mutually recursive, so we can't just build up the variables' graphs one by one:

(defvar main
  (let ((zig (cons 0 zag))
        (zag (cons 1 zig)))
    zig))       
      

Of course, not everything can be helped by this:

(defvar silly-list
  (let ((xs xs))
    (cons 1 xs)))
      

So we'll add a gnode subclass for temporarily storing let-bound variable occurances, and replace them after the fact. Unfortunately, this also causes the code that translates from expr to gnode to become a little spaghetti-y. On the other hand, we don't implement lambda lifting, as it's not strictly essential — the programmer will have to do it by hand, by writing top-level functions instead.

Making it tick

There are three parts to making reductions work: first, a way to do pattern matching against function alternatives. Second, given a mapping from this match, instantiating a function definition by replacing var-gnodes. The third part is orchestrating all of this by taking care of choosing which nodes to reduce.

Pattern matching is a relatively straightforward matter: a variable pattern always succeeds (and binds the subgraph) and a constructor pattern can either succeed and recurse, fail, or (if the actual node is a function application) force reduction. This latter is done via raising a Lisp condition.

Once we have the bindings in the format returned by match-pattern, we can easily instantiate function bodies, we just have to maintain a mapping from old node to new to avoid diverging on cycles.

Actual reduction then becomes just a matter of putting these two modules together. Several functions are provided with varying granularity: reduce-graph tries direct reduction, reduce-graph* catches need-reduce conditions and recurses on those nodes, in effect making sure a single reduction step at the target site can be made; and reduce-to-whnf repeatedly uses reduce-graph* until the head is either a constructor, or a non-saturated function application. simplify-apps is not really a reduction step, it just removes superfluous apply-gnodes.

Housekeeping

The rest of the code just keeps a registry of functions and constructors, and defines some primitive functions (note how we need the very simple bool ADT to be a built-in just so we have a return type for >=).

Putting it all together

Given an S-expression containing an Alef program, we can transform it into a graph suitable for reduction by doing the following steps:

1. Split into datatype definitions, variable definitions and function definitions
2. Process datatype definitions by registering the constructor names (since we don't do typechecking yet, the only information needed about constructors is that they are not function calls/variable references)
3. Register top-level variable names
4. Register function names
5. Process top-level variable definitions into graphs
6. Process function definitions into graph templates
7. Return the graph of the top-level variable called main as the actual program

Visualization

The nice plots in this blogpost were created by dumping the program's graph in GraphViz format, and running dot on the output. The visualization code is a straightforward traversal of the graph. Note how we store a stable name (generated using gensym) in each node, to ensure a correspondence in the generated GraphViz nodes between reduction steps. In the future, this could be used to e.g. animate the graph to show each reduction step.

We can use this like so:

(in-fresh-context
  (let ((g (parse-program '((defvar main (string-append "Hello, " "world!"))))))
    (simplify-apps g)
    (with-open-file (s "hello.dot" :direction :output :if-exists :supersede)
      (dot-from-graph g s))
    (reduce-to-whnf g)
    (with-open-file (s "hello-reduced.dot" :direction :output :if-exists :supersede)
      (dot-from-graph g s))))
    

Which results in the very uninteresting graphs:

and

In conclusion

SLOCCount tells me the whole code presented in this blogpost is 471 lines of Common Lisp; you can check out the full source code on GitHub. It implements lazy semantics for a pure functional programming language with pattern matching on algebraic datatypes; of course, by changing the definition of reduce-function, we could easily make it strict.

Next time

In my next blog post, I'll be adding Hindley-Milner type inference / typechecking. Because of the type-erasure semantics of our language, we could implement our evaluator without any type system implementation, simply by assuming the input program to be well-typed. So all that we'll need is an extra typechecking step between parsing and graph building that either rejects or accepts an Alef program.